ウェアと汗と雨と寒さ

登山の防寒についていろいろ考えると、いろいろな疑問に突き当たります。
その一つが、汗冷えの問題。

”化繊は乾くからいい。でも稜線では気化熱で冷えて寒い。”
”メリノウールは濡れても中々乾かないけど、暖かい。でも夏は気化熱で涼しい。”

濡れているのに暖かい？発熱するからとかいろいろありますが、それなら夏は暑いですよね。
夏は気化熱のほうが大きくなるから涼しくなるということ？
気化熱が問題なら、そもそも洋服のどこかでは気化しているわけだし、
ベースレイヤが何であろうがその分寒くはなっているはず。
むしろ寒くらないためには、気化しない透湿性の無い服が有利になる？そんなはずはないですよね。

他にも

”雨でぬれると冷えてしまう。これは空気よりも水の熱伝導率が高いからだ。”

なるほど。しかし下着一枚濡れていると、上にいくら着ても寒いことがあります。
上にたっぷり空気の膜があるのだから熱は逃げないはずなのに。

一体どういうことなのだろうと、調べていたところいくつかの考え方が見えてきました。

ニュートン冷却の法則

一つ目がニュートン冷却の法則です。

本来は、液体や気体などの媒質中におかれた高温の固体が媒質によって冷却される様子を表した法則ですが、「気体」→「外気」、「高温の個体」→「人」と置き換えれば、簡易的ながら山で凍える人から熱が逃げだす状況を定式化できます。

文献によっては表記がいろいろ異なりますが、今回考えやすい表記は次のようになります。

$$ΔQ=-\frac{αS(T_s – T_a)}{L}$$

$$ΔQ : 肌から奪われる時間当たりの熱量\\
T_s : 肌の表面温度\\
T_a :外気温\\
α : 熱伝導率\\
S : 肌と外気の触れる面積\\
L : 肌と外気の距離
$$

説明すると、肌から奪われる時間当たりの熱量は、
「肌の表面温度と外気温の温度差」と「肌と外気の間の熱伝導率」と「肌と外気の触れる面積」に比例し、
「肌と外気の距離」に反比例する、
ことがわかります。

これは何となく経験則的に理解できます。
外気が寒いほど、また接する面積が広いほど冷えるのが早いですし、
熱伝導率が高いもの（水や金属）に触れているほうが冷えやすい。

よく水の熱伝導率は空気の24倍もあるからなどと言っているのは、この熱伝導率のことです。

フーリエの法則と熱伝導方程式

もう一つの式が、フーリエの法則と熱伝導方程式です。
までどのように温度が変化していくかを計算することができます。

一次元（肌→外気の方向のみ）で考えた時の、熱伝導方程式は次のような感じ（になるはず）

$$ C_v\frac{\partial{T}}{\partial{t}} = α\frac{\partial^2{T}}{\partial{x^2}}\\
α : 熱伝導率\\
C_v : 単位体積熱容量
$$

時間変化と距離の変化の二つが混ざっているので、このままだと良くわかりません。先ほどの肌温度と外気の温度を入れて、温度変化が落ち着いた状態の境界問題を解くと次のようになります。

$$T = T_a + (T_s – T_a)(1 – \frac{x}{L})\\
x : 肌からの距離 ( 0 \leq x \leq L) \\
T : 肌から距離 ｘ の場所の温度
$$

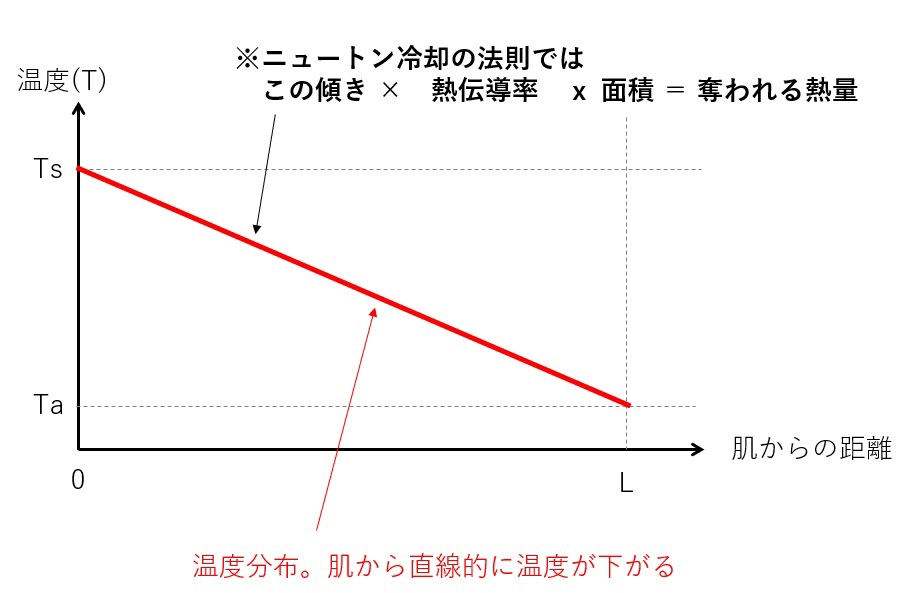
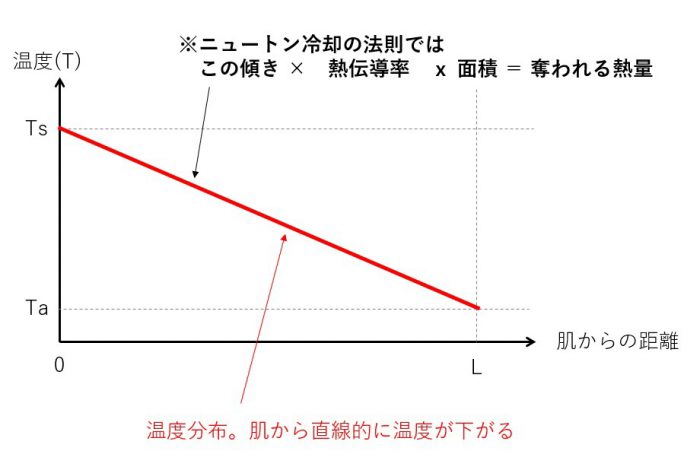
簡単に言えば、肌から外気まで線形に温度は下がっていく。という単純な結果です。
厳密にいうと、肌から距離Lのところが外気温であるわけではない、たとえ厚さLのウェアを着ていても、さらに距離Lから熱を大気中に放出しますので、xは半無限距離として最後は緩やかに変化していくのですが、面倒なのでここでは考えません！

グラフを描くとこんな感じ。とてもシンプルです。

このグラフをかくときのポイントは、
もし熱伝導率αが同じだとすると、Lが大きいほど傾きが緩やかになり、出ていく熱量が減ることです。

気化熱を考えに入れてみる

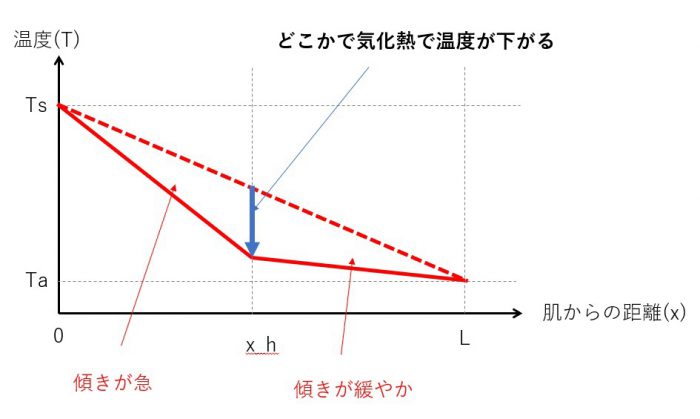
さて、ここで気化熱です。厚さLのウェア中のどこかで熱量が気化熱によって奪われていると考えます。

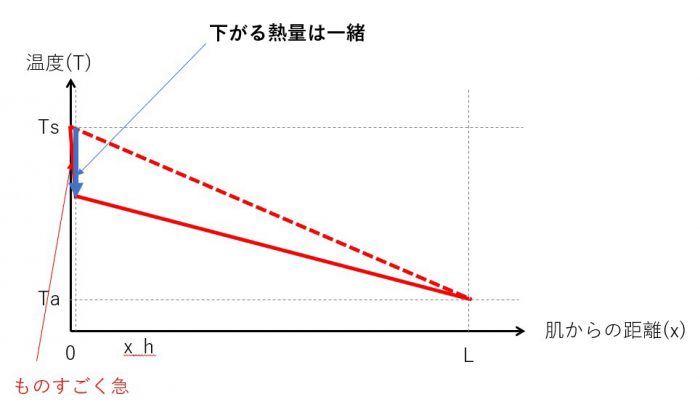
この気化熱で熱を奪われる個所を、肌からの距離 x_h とします。肌から伝わってくる熱量のうち、一部は気化熱へ、一部は熱伝導によって外気へ伝わっていくと考えると、熱伝導のグラフはこんな感じに変化すると想定されます。

同じ熱伝導率のときには傾きが大きいほど熱量が大きくなりますから、肌からは今までよりもたくさんの熱量が奪われることが分かります。一方で傾きが少なくなる外気側は熱量が減ります。

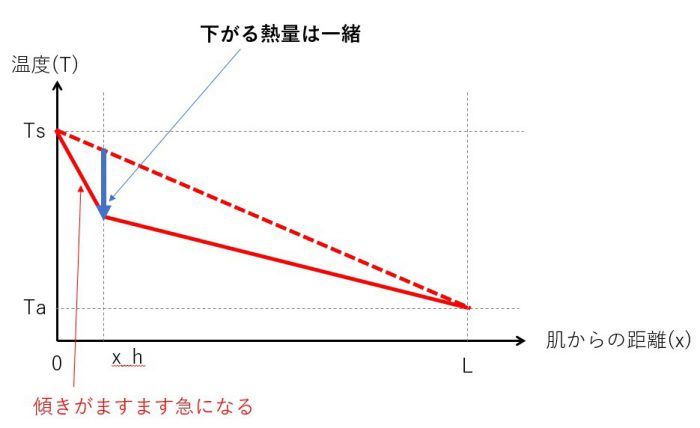
さて、では x_h がの場所が変化したらどうなるでしょうか。それが次のグラフです。

見てわかる通り、気化熱で奪われる熱量が一定とすると、熱伝導率と面積が同じですから、気化する場所が肌に近いほど温度差が大きくなって、出ていく熱量が大きくなります。

つまり、肌付近で気化すると寒く感じるということになります。どこかで気化しているのだから奪われる熱量は同じでしょ？と思っても、気化する場所によって肌から奪われる熱量が変化するんですね。

おまけに気化する際の熱量は、外気温に依らず一定とすると、肌のすぐそばで気化されるとこんな状況にもなり得ます。

一応素肌の状態でも、無風なら空気膜としてL=3～4mm程度あるそうなので、服を脱いだほうがまだ暖かい場合もあります。

濡れた下着を着続けることが、奪われる熱量を増やし、山ではどんなに危険なことかわかると思います。

濡れても暖かいわけを考える

メリノウールでは濡れていても暖かい理由は何でしょうか。

先ほどまでは熱伝導率が同じものとしていましたが、今度は24倍の熱伝導率を持つ水の膜がウェアの中にできてしまった状態を考えます。

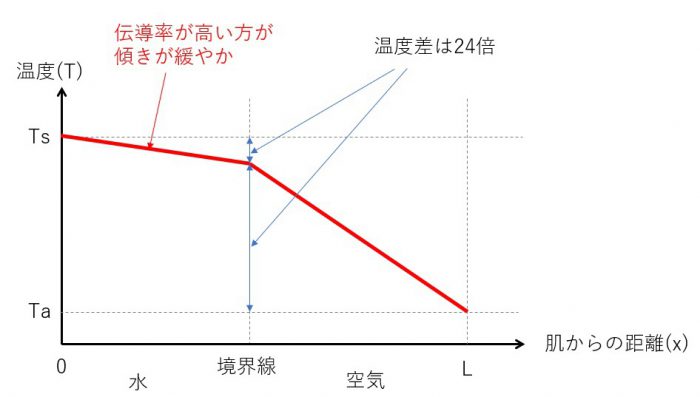
熱伝導率が2層に分かれている場合、熱伝導方程式を貼り合わせることになりますが、その境界温度はニュートンの冷却の方式から、逃げる熱量をΔQを一定にしますから、αが24倍ある分、Ts  – Ta が1/24になります。グラフでかくとこんな感じになります。

境界の温度は実は熱伝導率が高い側が高くなりますね。水が肌からの熱で温まってしまっていると考えるとわかりやすいです。傾きが緩やかでも二つを合わせた熱伝導率は下がってしまっているので水が無い方が暖かいのですが、もし水の層が十分に薄ければ、全体の熱伝導率も落ちませんし寒さには大きく影響しない。と考えることができそうです。

つまり厚着の場合、水の層ができていて一番問題だったのは気化熱のようです。濡れた服にサランラップを巻くと暖かいというようなことも同じ原理と思われます。たとえ濡れていても気化して熱を奪われなければそんなに問題ではない。。と考えられそうです。逆に夏で薄着だと水の膜の大きさが全体の厚さLに対して十分厚くなりますから、逃げる熱量も増えて熱伝導率も効いてきます。

つまり、メリノウールは湿気を取り込む性質はあるものの、表面は撥水していて保水しません。おそらくあまり気化させないため、濡れていても寒くは感じないのです。では汗はどこに行くのかというと、このあたり考え方が難しいのですが、自ら気化しない代わりにより上位のウェアに水を渡してしまうのでしょう。

化繊は積極的に気化しますし、上位のレイヤに水を渡していくため、乾きやすいものの気化熱で寒い。

綿は気化しますし、保水して上位のレイヤにすら水を渡さないので、ひたすら気化だけで水を処理してしまう。乾きにくいし長時間にわたって気化熱で寒い。

と考えることができるわけです。

（追記）メリノウール自体は気化させるのですが、湿気を取り込んで繊維から気化させることで、肌から離れたところで気化させる働きになるようです。つまり、若干上位レイヤに水を渡して、気化させていくという動きに近いことをメリノウール単体で行っているわけですね。一方綿などは保水しつつ周りも濡れているため、肌表面から直接気化していくような動きとなり急激に熱が奪われる、というわけです。

結論：汗が乾かなそうなときはメリノウールを入れておく→ドライレイヤーを使う

では何がいいのかというところを考えます。

ベストは、水の膜ができないように、汗をどんどん上位レイヤに渡して肌からできるだけ遠いところで気化してもらうというパターンです。このために透湿性だとかいろいろレイヤリングを工夫するところだと思います。

ただ、どうしても汗処理には限界があります。さらに気温が低いときには気化しにくい、乾きづらいという問題もあります。こうなると水の膜ができることを覚悟の上でレイヤリングを考えます。

そうするとたとえ濡れても寒くならない、メリノウールを肌付近に入れておく、というのがベストな解になるわけです。

化繊とメリノウールのどちらがいいかという議論はよくありますが、たとえ雨でずぶぬれになっても冷えにくいメリノウールが安心といわれのもなるほどというわけです。

（追記）今は汗をかいても肌を濡らさないドライレイヤーの製品がいくつも出ています。これと汗を吸い上げてくれるベースレイヤを組み合わせるのが個人的にはベストな解になりました。

※仮説ですので、登山のウェアリングは    自己責任の下十分ご注意ください。